Continuous Charge Distribution
We have so far dealt with charge configurations involving discrete
charges q1, q2, ...,
qn. One reason why we restrict to discrete charges is that
the mathematical treatment is simpler and does not involve calculus. For many
purposes, however, it is impractical to work in terms of discrete charges and
we need to work with continuous charge distributions. For example, on the
surface of a charged conductor, it is impractical to specify the charge
distribution in terms of the locations of the microscopic charged constituents.
It is more feasible to consider an area element 
as shown in the figure. On the surface of
the conductor (which is very small on the macroscopic scale but big enough to
include a very large number of electrons) and specify the charge 
Q on that element.
We then define a surface charge density s at the area element by
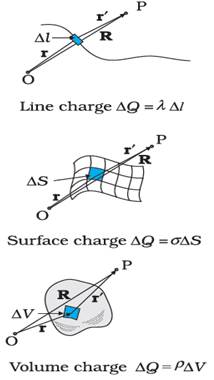
We can do this at different points on the conductor
and thus arrive at a continuous function 
, called the surface charge density. The
surface charge density so defined ignores the quantisation
of charge and the discontinuity in charge distribution at the microscopic
level. At the microscopic level, charge distribution is discontinuous,
because they are discrete charges separated by intervening space where there is
no charge. represents
macroscopic surface charge density, which in a sense, is a smoothed out average
of the microscopic charge density over an area element S which,
as said before, is large microscopically but small macroscopically. The units
for are C/m2.
Similar considerations apply for a line charge
distribution and a volume charge distribution. The linear charge density 
of a wire is defined by
where 
is a small line element of wire on the
macroscopic scale that, however, includes a large number of microscopic charged
constituents, and 
is the charge contained in that line element.
The unit for is C/m. The volume charge density (sometimes
simply called charge density) is defined in a similar manner:
where Q is the charge
included in the macroscopically small volume element V that includes a
large number of microscopic charged constituents. The units for 
are C/m3.
The notion of continuous charge distribution is similar to that we
adopt for continuous mass distribution in mechanics. When we refer to the
density of a liquid, we are referring to its macroscopic density. We regard it
as a continuous fluid and ignore its discrete molecular constitution. The field
due to a continuous charge distribution can be obtained in much the same way as
for a system of discrete charges. Suppose a continuous charge distribution in
space has a charge density
. Choose any convenient origin O and let the
position vector of any point in the charge distribution be r. The charge density r may vary from point to point, i.e., it is a
function of r. Divide the charge distribution into small volume elements of
size V. The charge in a
volume element V is 
V.
Now, consider any general point P (inside or outside the
distribution) with position vector R as shown in the figure. Electric field due
to the charge V is given by
Coulomb’s law:
where 
is the distance between the charge element and
P and
is a unit vector in the direction from the
charge element to P. By the superposition principle, the total electric field
due to the charge distribution is obtained by summing over electric fields due
to different volume elements:
Note that 
all can vary from point to point. In a strict
mathematical method, we should let 
and the sum then becomes an integral; but we
omit that discussion here, for simplicity. In short, using Coulomb’s law and
the superposition principle, electric field can be determined for any charge
distribution, discrete or continuous or part discrete and part continuous.
|
|
|
|
