Electric Field

Electric Field:

Electric field due to a charge is the space around the test charge in which it experiences a force. The presence of an electric field around a charge cannot be detected unless another charge is brought towards it.

Electric field at a point is measured in terms of electric field intensity. Electric field intensity at a point in an electric field is defined as the force experienced by a unit positive charge kept at that point. It is a vector quantity with the unit of N C^{-1 .}

=

Let us consider a point charge Q placed in vacuum, at the origin O. If we place another point charge q at a point P, where OP = r, then the charge Q will exert a force on q as per Coulomb’s law. We may ask the question: If charge q is removed, then what is left in the surrounding? Is there nothing? If there is nothing at the point P, then how does a force act when we place the charge q at P.

In order to answer such questions, the early scientists introduced the concept of field. According to this, we say that the charge Q produces an electric field everywhere in the surrounding. When another charge q is brought at some point P, the field there acts on it and produces a force. The electric field produced by the charge Q at a point r is given as

------ (1)

where = , is a unit vector from the origin to the point ||. Thus, Equation (1) specifies the value of the electric field for each value of the position vector r. The effect of the charge has been incorporated in the existence of the electric field. We obtain the force F exerted by a charge Q on a charge q, as

------ (2)

If we denote the position of charge q by the vector , it experiences a force F equal to the charge q multiplied by the electric field E at the location of q. Thus,

() = q () ------ (3)

Electric field due to point charge:

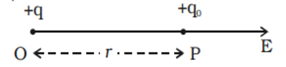
Electric field due to a point charge

Let q be the point charge placed at O in air (above figure). A test charge q_o is placed at P at a distance from q. According to Coulomb’s law, the force acting on q_o due to q is

The electric field at a point P is, by definition, the force per unit test charge.

The direction of E is along the line joining O and P, pointing away from q, if q is positive and towards q, if q is negative.

In vector notation where is a unit vector pointing away from q.

Electric field due to system of charges:

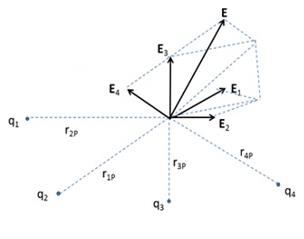
If there are a number of stationary charges, the net electric field (intensity) at a point is the vector sum of the individual electric fields due to each charge.

Electric field E₁ at due to q₁ at ₁ is given by

₁ =

where is a unit vector in the direction from q₁ to P, and _1P is the distance between q₁ and P.

In the same manner, electric field E₂ at r due to q₂ at ₂ is

₂ =

where is a unit vector in the direction from q₂ to P and _2P is the distance between q₂ and P. Similarly writing equations for ₃ , ₄ , . . . . . . ,_n due to the charges q₂, q₃, . . . . . ., q_n. Then by the superposition principle, the electric field at r due to the system of charges is given as,

() = ₁() + ₂() + … + _n()

() = + + . . . . . . . +

() = _tp

Here is a vector quantity that varies from one point to the other. It is determined by the positions of source charges.

Electric Field Lines

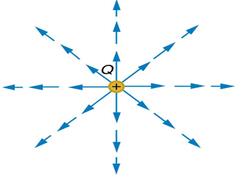
Electric field is a vector quantity and can be represented as vectors. Let the point charge be placed at the origin as shown in the figure (a).

(a)

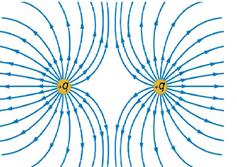
(b)

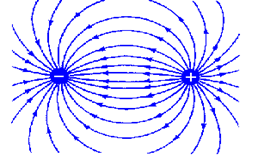
(c)

Draw vectors pointing along the direction of the electric field with their lengths proportional to the strength of the field at each point. Since the magnitude of electric field at a point decreases inversely as the square of the distance of that point from the charge, the vector gets shorter as one goes away from the origin, always pointing radially outward. In this figure, each arrow indicates the electric field, i.e., the force acting on a unit positive charge. E is strong near the charge, so the density of field lines is more near the charge and the lines are closer. Away from the charge, the field gets weaker and the density of field lines is less, resulting in well-separated lines.

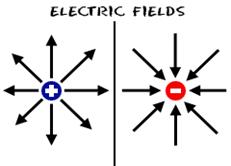
Figure (b) shows how the electric field react for the like charges and figure (c) shows how the electric field respond for unlike charges. In case of like charges, they repel each other where as in case of unlike charges, the attract each other.

Properties of electric field lines:

I. Lines of force start from positive charge and terminates at negative charge.

II. Lines of force never intersect each other.

III. In a charge-free region, electric field lines can be taken to be continuous curves without any breaks.

IV. The tangent to a line of force at any point gives the direction of electric field (E) at that point.

V. The number of lines per unit area, through a plane at right angles to the lines, is proportional to the magnitude of E. This means that, where the lines of force are closer together, E is large and where they are far apart, E is small as mentioned above in earlier topic.

VI. Each unit positive charge gives rise to lines of force in free space. Hence number of lines of force originating from a point charge q is N= in free space.