Electric Dipole

Electric Dipole:

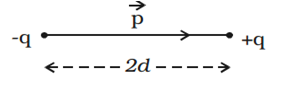
Two equal and opposite charges separated by a very small distance say 2d constitute an electric dipole as shown in the above figure. The line connecting the two charges defines a direction in space. The direction from –q to q is said to be the direction of the dipole. The mid-point of locations of –q and q is called the centre of the dipole.

Water, ammonia, carbon-di-oxide and chloroform molecules are examples of permanent electric dipoles. These molecules have centres of positive and negative charges which do not coincide with each other and are separated by a small distance. Hence they are called as electric dipoles.

Dipole moment is given by the product of the magnitude of the one of the charges and the distance between them. Then the dipole moment is given as

Dipole moment is a vector quantity and its unit is C m (Coulomb meter).

Electric field due to an electric dipole at a point on its axial or axis line:

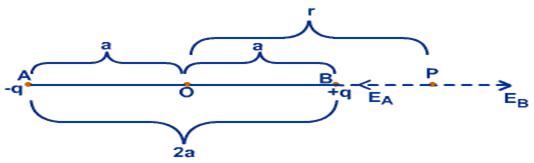
From the above diagram, AB is an electric dipole of two point charges –q and +q separated by a small distance of 2a. P is a point along the axial line of the dipole at a distance r from the midpoint O of the electric dipole.

The electric dipole at the point P due to +q placed at B is,

E₁ = (along BP)

The electric field at the point P due to –q placed at A is,

E₂ = (along PA)

Here E₁ and E₂ act in opposite directions.

The magnitude of resultant electric field (E) acts in the direction of vector with a greater magnitude. The resultant electric field at P is,

E = E₁ + ( - E₂ )

E = (along BP)

E = (along BP)

E = (along BP)

If the point P is far away from the dipole, then a << r

E =

E =

E = (along BP) [ p= q 2a]

Here E acts in the direction of dipole moment.

Electric field due to an electric dipole at a point on an equatorial line:

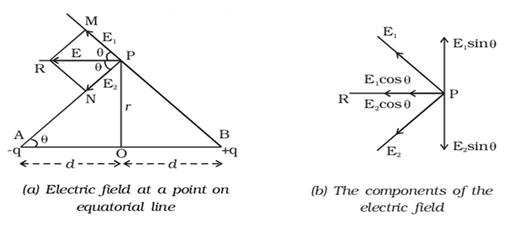
Consider an electric dipole AB. Let 2d be the dipole distance and p be the dipole moment. P is a point on the equatorial line at a distance r from the midpoint O of the dipole as shown in the above figure.

Electric field (E) at a point P due to the charge +q of the dipole is given as,

E₁ = along BP

E₁ = along BP ( )

Electric field (E₂) at a point P due to the charge –q of the dipole is given by,

E₂ = along PA

E₂ = along PA

The magnitudes of E₁ and E₂ are equal. Resolving E₁ and E₂ into their horizontal and vertical components as shown in figure (b), the vertical component E₁ and E₂ are equal and opposite, therefore they cancel each other.

The horizontal components E₁ and E₂ will get added along PR.

Resultant electric field at the point P due to the dipole is

E = E₁ (along PR)

E = 2 E₁ (since E₁ = E₂ )

E = 2

But =

E =

E =

E = ( since p = q2d )

For a dipole, d is very small when compared to r. Hence

E =

The direction of E is along PR, parallel to the axis of the dipole and opposite to the direction of dipole moment.

Electric dipole in a uniform electric field and its torque:

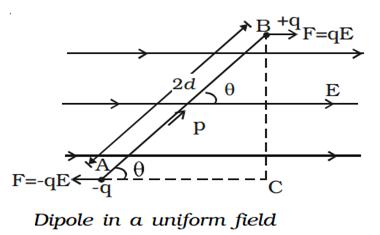
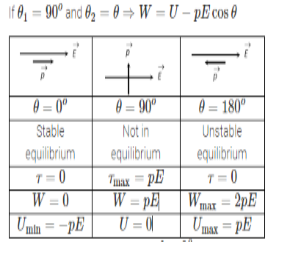
Consider a dipole AB of dipole moment p placed at an angle in an uniform electric field E as shown in the figure. The charge +q experiences a force qE in the direction of the field. The charge –q experiences an equal force but in the opposite direction. Thus the net force on the dipole is zero. The two equal and unlike parallel forces are not passing through the same point, resulting in a torque on the dipole, which tends to set the dipole in the direction of the electric field.

The magnitude of torque is,

=

= (since

The vector notation is given as

=

If the dipole is placed in a non-uniform electric field at an angle , in addition to a torque, it experiences a force.

QUANTITES	EQUIVALENTS
q	ne
e	1.6 C (Coulomb)
F
k
	8.854 C^2N^-1m^-2
	9 N m^2C^-2
F
	C m
	C/m^2
	C/m
	C/m^3
E (axial)
E (equatorial)
	One of the force × Perpendicular distance between the forces