Kirchhoff’s Law

Gustav Kirchhoff developed a set of laws relating to the conservation of current and energy in the electrical circuits. They are KCL (Kirchhoff’s Current Law) which deals with the current flowing in the circuit and KVL (Kirchhoff’s Voltage Law) which deals with the voltage source present in the circuit. His discoveries has also paved the path for quantum theory of electromagnetic induction by Max Planck. Most of his discoveries and researches were dealing with electric current. Among this Kirchhoff’s law of circuits is the most important one.

Georg Simon ohm showed the relationship between voltage, current and resistance and formulated the ohm’s law. This law is the basis of electricity. The law states that V = I R, where voltage V is in volts, Current I in amps and resistance R in ohms. Thus I = and R = . But in complex circuits it is difficult to find the voltage and current in the circuit by using Ohm’s law. Hence for complex circuits Kirchhoff’s law of circuits help us to find the value of voltage and current which flows within the circuit.

Kirchhoff’s first law or Kirchhoff’s junction law or Kirchhoff’s current law:

The algebraic sum of the currents meeting at a junction in a closed electric circuit is zero, i.e.,

Consider a junction O in the electrical circuit at which the five conductors are meeting. Let be the currents in these conductors in directions, shown in figure,

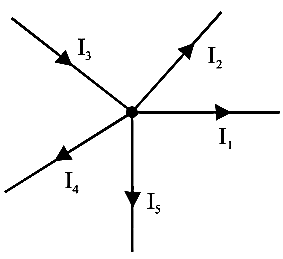
Let us adopt the following sign convention: the current flowing in a conductor towards the junction is taken as positive and the current flowing away from the junction is taken as negative.

According to Kirchhoff’s first law, at junction O

i.e., total current flowing towards the junction is equal to total current flowing out of the junction.

Current cannot be stored at a junction. It means, no point/ junction in a circuit can act as a source or sink of charge.

Kirchhoff’s first law supports law of conservation of charge.

Kirchhoff’s Second law or Kirchhoff’s loop law or Kirchhoff’s voltage law:

The algebraic sum of changes in potential around any closed path of electric circuit (or closed loop) involving resistors and cells in the loop is zero, i.e.,

In a closed loop, the algebraic sum of the emfs and algebraic sum of the products of current and resistance in the various arms of the loop is zero, i.e.,

Kirchhoff’s second law supports the law of conservation of energy, i.e., the net change in the energy of a charge, after the charge completes a closed path must be zero.

Kirchhoff’s second law follows from the fact that the electrostatic force is a conservative force and work done by it in any closed path is zero.

Consider a closed electrical circuit as shown in figure, containing two cells of emfs. and and three resistors of resistances , and

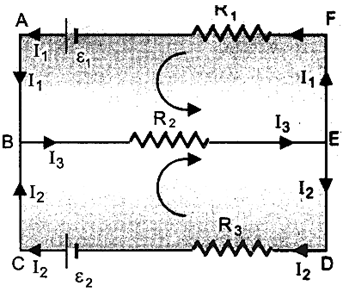
We adopt the following sign convention: Traverse a closed path of a circuit once completely in clockwise or anticlockwise direction.