Combination of Lens

Consider two lenses A and B of focal length f₁ and f₂ placed in contact with each other. Let the object be placed at a point O beyond the focus of the first lens A). The first lens produces an image at I₁.

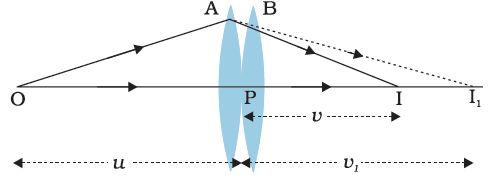
Since image I₁ is real, it serves as a virtual object for the second lens B, producing the final image at I. It must, however, be borne in mind that formation of image by the first lens is presumed only to facilitate determination of the position of the final image. In fact, the direction of rays emerging from the first lens gets modified in accordance with the angle at which they strike the second lens.

Since the lenses are thin, we assume the optical centres of the lenses to be coincident. Let this central point be denoted by P. For the image formed by the first lens A, we get

------ (i)

For the image formed by the second lens B

We get

------ (ii)

Adding Eqs (1) and (2),we get

------ (iii)

If two lens-system is regarded as equivalent to a single lens of focal length f,we have

So that we get

------ (iv)

The derivation is valid for any number of thin lenses in contact. If several thin lenses of focal length f₁, f₂, f₃,... are in contact, the effective focal length of their combination is given by

------ (v)

In terms of power Eq(5) can be written as

------ (vi)

where P is the net power of the lens combination. The sum is an algebraic sum of individual powers, so some of the terms on the right side may be positive (for convex lenses) and some negative (for concave lenses).

Combination of lenses helps to obtain diverging or converging lenses of desired magnification. It also enhances sharpness of the image. Since the image formed by the first lens becomes the object for the second, implies that the total magnification m of the combination is a product of magnification of individual lenses

------ (vii)

Such a system of combination of lenses is commonly used in designing lenses for cameras, microscopes, telescopes and other optical instruments.