Refraction Through a Prism

The above figure shows the passage of light through a triangular prism ABC. The angles of incidence and refraction at the first face AB are i and r₁, while the angle of incidence (from glass to air) at the second face AC is r₂ and the angle of refraction or emergence e. The angle between the emergent ray RS and the direction of the incident ray PQ is called the angle of deviation, .

In the quadrilateral AQNR, two of the angles (at the vertices Q and R) are right angles. Therefore, the sum of the other angles of the quadrilateral is 180°.

From the triangle QNR ,

On comparing these two equations, we get,

------ (i)

The total deviation is the sum of deviations at the two faces,

------ (ii)

Thus, the angle of deviation depends on the angle of incidence. A plot

between the angle of deviation and angle of incidence is shown in the figure.

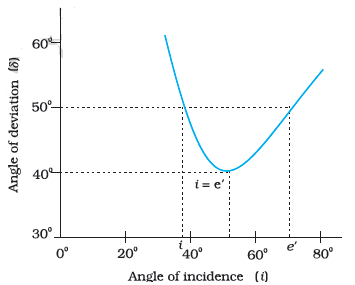
At the minimum deviation D_m, the refracted ray inside the prism becomes parallel to its base. We have

= D_m, i = e which implies r₁ = r₂

Equation (i) gives

------ (iii)

------ (iv)

The refractive index of the prism is

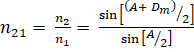------ (v)

The angles A and D_m can be measured experimentally. Equation (v) thus provides a method of determining refractive index of the material of the prism.

For a small angle prism, i.e., a thin prism, D_m is also very small, and we get

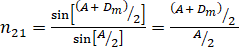
It implies that, thin prisms do not deviate light much.