Diffraction

Diffraction is defined as the bending of light around the corners of an obstacle or aperture into the region of geometrical shadow of the obstacle. It is due to interference of waves according to the Huygens–Fresnel principle. These characteristic behaviors are exhibited when a wave encounters an obstacle or a slit that is comparable in size to its wavelength.

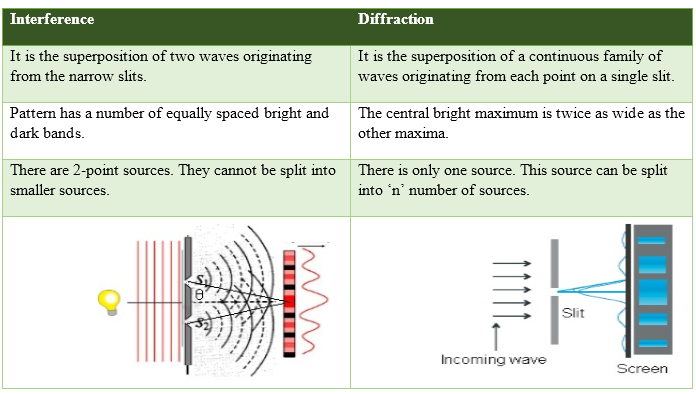
Single slit experiment

When single narrow slit is illuminated by a monochromatic source, a broad pattern with a central bright region is seen. On both sides, there are alternate dark and bright regions, the intensity becoming weaker away from the centre.

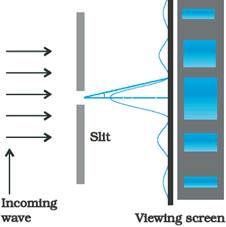
Let us consider a parallel beam of light falling normally on a single slit LN of width a. The diffracted light meets a screen. The midpoint of the slit is M. MC is perpendicular to the slit.

Consider the intensity at a point P on the screen.

The slit is further divided into smaller parts, whose midpoints are M₁, M₂ etc. Straight lines joining P to the different points L, M, N, etc., can be treated as parallel, making an angle θ with the normal MC.

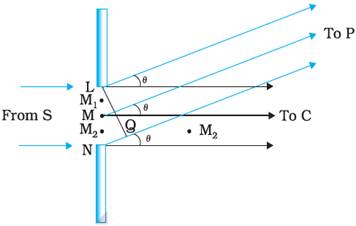
Different parts of the wave front can be treated as secondary sources.

Since the incoming wave front is parallel to the plane of the slit, these sources are in phase.

The path difference NP – LP between the two edges of the slit will be

NP – LP = NQ = a sin θ ≈ aθ

Similarly, if two points M₁ and M₂ in the slit plane are separated by y, the path difference will be

M₂P – M₁P = yθ

Equal, coherent contributions from a large number of sources, each with a different phase need to be summed up.

Explanation for position of minima in diffraction pattern

The minima (zero intensity) occurs at,

θ =

where, n = ±1, ±2, ±3, ....

Consider the angle θ where the path difference aθ is λ. Then,

θ ≈ 

Now, divide the slit into two equal halves LM and MN each of size . For every point M₁ in LM, there is a point M₂in MN such that M₁M₂ = . The path difference between M₁ and M₂ at P,

That is, the contributions from M₁ and M₂ are 180º out of phase and cancel each other, when,

θ =

Therefore, contributions from the two halves of the slit LM and MN, cancel each other. The intensity is also zero for,

θ =

where, n is any integer (≠ 0).

The angular size of the central maximum increases when the slit width a decreases.

Explanation for position of maxima in diffraction pattern

At the central point C on the screen, the angle θ is zero. All path differences are zero and hence all the parts of the slit contribute in phase. This gives maximum intensity at C. Other secondary maxima are shown at,

and they go on becoming weaker and weaker with increasing n.

Consider an angle

which is midway between two of the dark fringes.

Divide the slit into three equal parts. If we take the first two thirds of the slit, the path difference between the two ends would be

The first two-thirds of the slit can therefore be divided into two halves which have a path difference of . The contributions of these two halves cancel as described earlier. Only the remaining one-third of the slit contributes to the intensity at a point between the two minima. This will be much weaker than the central maximum, where the entire slit contributes in phase.

We can similarly show that there are maxima at

where, n = 2, 3, etc.

These become weaker with increasing n, since only one-fifth, one-seventh, etc., of the slit contributes in these cases.

Double slit vs single slit patterns

In the double-slit experiment, we must note that the pattern on the screen is actually a superposition of single-slit diffraction from each slit or hole, and the double-slit interference pattern. It shows a broader diffraction peak in which there appear several fringes of smaller width due to double-slit interference.

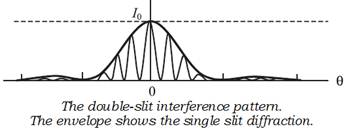
The number of interference fringes occurring in the broad diffraction peak depends on the ratio , that is the ratio of the path difference to the width of a slit. In the limit of ‘a’ becoming very small, the diffraction pattern will become very flat and we will observe the two-slit interference pattern.

Interference vs diffraction due to single slit

(i) The interference pattern has a number of equally spaced bright and dark bands. The diffraction pattern has a central bright maximum which is twice as wide as the other maxima. The intensity falls as we go to successive maxima away from the centre, on either side.

(ii) We calculate the interference pattern by superposing two waves originating from the two narrow slits. The diffraction pattern is a superposition of a continuous family of waves originating from each point on a single slit.

(iii) For a single slit of width a, the first null of the interference pattern occurs at an angle of. At the same angle of , we get a maximum (not a null) for two narrow slits separated by a distance ‘a’.

Constraints for diffraction due to single slit

i. a and d have to be small

ii. D has to be large

iii. Source must be monochromatic

Viewing the diffraction pattern

The diffraction pattern can be viewed by putting two razor blades touching each other in front of a filament. If filter for red or blue light are used (for monochromatic source), the fringes can be seen clearly.

We should not use direct sunlight – it can damage the eye and will not give fringes anyway as the Sun subtends an angle of  on the eye.

Energy is conserved during interference and diffraction

In interference and diffraction, light energy is redistributed. If it reduces in one region, producing a dark fringe, it increases in another region, producing a bright fringe. There is no gain or loss of energy, which is consistent with the principle of conservation of energy.