Resolving Power of an Objective Lens

The resolving power of an objective lens is measured by its ability to differentiate two lines or points in an object. The greater the resolving power, the smaller the minimum distance between two lines or points that can still be distinguished.

A parallel beam of light falling on a convex lens, because of diffraction, instead of getting focused to a point gets focused to a spot of finite area.

The pattern on the focal plane consists of a central bright region surrounded by concentric dark and bright rings.

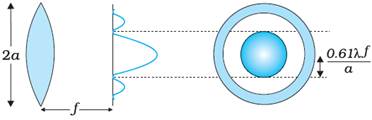
The radius of the central bright region is approximately

$r_{o} = \frac{1.22 λ f}{2 a} = \frac{0.61 λ f}{a}$

Although the size of the spot is very small, it affects the limit of resolution of optical instruments like a telescope or a microscope.

For the two stars to be just resolved,

$f Δ r_{o} = \frac{0.61 λ f}{a} \Rightarrow Δ = \frac{0.61 λ}{a}$

Thus Δθ will be small if the diameter of the objective is large. It is for this reason that for better resolution, a telescope must have a large diameter objective.

For a microscope the object is placed slightly beyond f, so that a real image is formed at a distance v. The magnification – ratio of image size to object size – is given by,

$m = \frac{v}{f}$

Also, ≈ 2tan β, where 2β is the angle subtended by the diameter of the objective lens at the focus of the microscope.

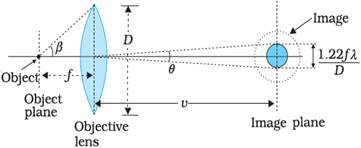
When the separation between two points in a microscopic specimen is comparable to the wavelength λ of the light, the diffraction effects become important. The image of a point object will again be a diffraction pattern whose size in the image plane will be

$vθ = v \frac{1.22 λ}{D}$

Two objects whose images are closer than this distance will not be resolved and will be seen as one. The corresponding minimum separation, d_min, in the object plane is given by

$d_{m i n} = \frac{1.22 λ}{D} \times \frac{v}{m}$

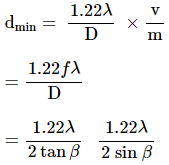
If the medium between the object and the objective lens has a refractive index n

$d_{m i n} = \frac{1.22 λ}{2 n sin β}$

Fresnel distance

The angle of diffraction due to an aperture (i.e., slit or hole) of size a illuminated by a parallel beam is . This is the angular size of the bright central maximum. In travelling a distance z, the diffracted beam acquires a width due to diffraction.

The distance beyond which the divergence of beam of width ‘a’ becomes significant is called Fresnel distance, at which point, is denoted by z_F

$\frac{z_{F} λ}{a} = a$

For distances much smaller than z_F, the spreading due to diffraction is smaller compared to the size of the beam. It becomes comparable when the distance is approximately z_F. For distances much greater than z_F, the spreading due to diffraction dominates over that due to ray optics (i.e., the size ‘a’ of the aperture). The ray optics is valid in the limit of wavelength tending to zero.