Interference of Light
Superposition
of two waves, travelling through the same medium, is called interference.
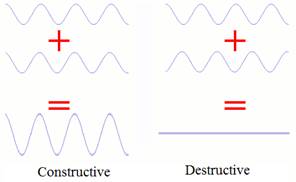
Constructive
interference occurs when the two interfering waves have
a displacement in the same direction and the amplitude of the resulting wave is
the addition of amplitudes of interfering waves.
Destructive
interference occurs when the two interfering waves have
a displacement in different direction (out of phase) and the amplitude of the
resulting wave is the difference of amplitudes of interfering waves.
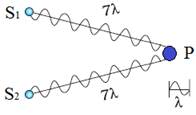
Consider
two coherent sources S1 and
S2 a
point P for which S1P
= S2P.
Since the distances S1P
and S2P
are equal, waves from S1 and
S2 will
take the same time to travel to the point P and waves that originate from S1 and
S2 in
phase will also arrive, at the point P, in phase.
If the
displacement produced by the source S1 at
the point P is given by
y1 = a
cos ωt
then, the
displacement produced by the source S2 (at
the point P) will also be given by
y2 = a
cos ωt
Thus,
the resultant of displacement at P would be given by
y = y1 + y2 = 2
a cos ωt
Since
the intensity is the proportional to the square of the amplitude, the resultant
intensity will be given by,
I = 4Io
where Io represents
the intensity produced by each one of the individual sources; Io is
proportional to a2.
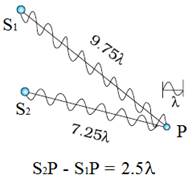
In fact
for all points where the phase difference is 2nπ or path difference is nλ, the interference will be constructive.
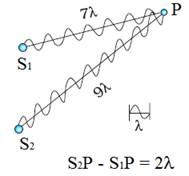
If the
phase difference is (2n + 1)π or path
difference is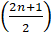 
λ, the interference will be
destructive.
For any
other arbitrary point let the phase difference between the two displacements be
φ.
y1 = a
cos ωt
y2 = a cos
(ωt + φ)
The
resultant displacement will be given by
y = y1 + y2 = a
[cos ωt + cos (ωt + φ]
Since φ is constant, the
amplitude of the resultant displacement is 2a cos 
.
Or the intensity I = 4Io cos2 
If the two sources are not coherent the average intensity
will be given by
<I> = 4Io <cos2 >
where angular brackets represent time averaging.
The function cos2 will randomly vary between 0 and 1 and the average
value will be 
.
The resultant intensity will be given by,
I = 2Io
|
|
|
|
