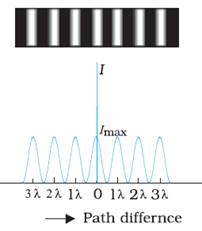
Young’s Double Slit Experiment

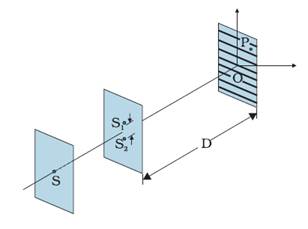
Thomas Young made two pinholes S₁ and S₂ (very close to each other) on an opaque screen. These were illuminated by another pinhole that was in turn, lit by a bright source. Light waves spread out from S and fall on both S₁ and S₂. S₁and S₂ then behave like two coherent sources because light waves coming out from S₁ and S₂ are derived from the same original source and any abrupt phase change in S will manifest in exactly similar phase changes in the light coming out from S₁ and S₂.

Thus, the two sources S₁ and S₂ will be locked in phase; i.e., they will be coherent like the two vibrating needles.

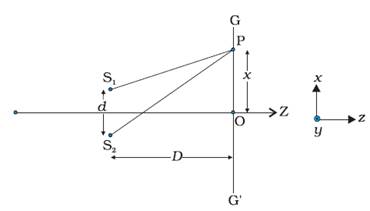
Spherical waves originating from S₁ and S₂ will produce interference fringes on the screen GG’.

For an arbitrary point P on the line GG’ to have a maximum,

S₂P – S₁P = nλ; n = 0, 1, 2 ...

From the geometry of the figure,

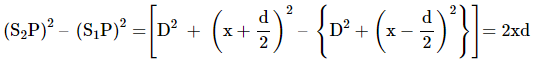
${(S_{2} P)}^{2} - {(S_{1} P)}^{2} = [D^{2} + {(x + \frac{d}{2})}^{2} - \{D^{2} + {(x - \frac{d}{2})}^{2}\}] = 2 x d$

which gives

$(S_{2} P - S_{2} P) (S_{2} P + S_{2} P) = 2 x d$

If x << D and d << D, then,

S₂P + S₂P ≈ 2D

$S_{2} P + S_{2} P \approx 2 D$

S₂P − S₂P =

For constructive interference or bright fringes,

$x_{n} = \frac{n λ D}{d} [n = 0, 1, 2 \dots .]$

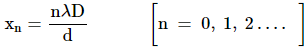
For destructive interference or dark fringes,

$x_{n} = (n + \frac{1}{2}) \frac{λ D}{d} [n = 0, 1, 2 \dots .]$

Fringe width in Double Slit Experiment

Dark and bright fringes are equally spaced and the distance between two consecutive bright fringes or two consecutive dark fringes is given by

$f r i n g e w i d t h, β = x_{n + 1} - x_{n} = \frac{λ D}{d}$

The central point O will be bright because S₁O = S₂O and it will correspond to n = 0. If we consider the line perpendicular to the plane of the paper and passing through O [i.e., along the y-axis] then all points on this line will be equidistant from S₁ and S₂ and we will have a bright central fringe which is a straight line.

All other fringes will be hyperbolas. If D >> β then they will be almost straight lines.