Mirror Formula
Mirror Formula:
If rays
emanating from a point actually meet at another point after reflection and/or
refraction, that point is called the image of the first point. The image is real if the rays actually converge to the point; it is virtual if the rays do not actually meet but appear to diverge
from the point when produced backwards.
An image is
thus a point-to-point correspondence with the object established through
reflection and/or refraction. In principle, we can take any two rays emanating
from a point on an object, trace their paths, find their point of intersection
and thus, obtain the image of the point due to reflection at a spherical
mirror.
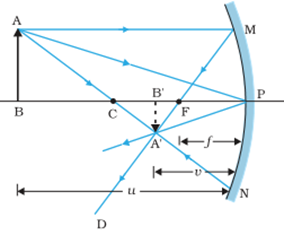
In practice, however, it is
convenient to choose any two of the following rays:
(i)
The ray
from the point which is parallel to the principal axis. The reflected ray goes
through the focus of the mirror.
(ii)
The ray
passing through the centre of curvature of a concave mirror or appearing to
pass through it for a convex mirror. The reflected ray simply retraces the
path.
(iii)
The ray
passing through (or directed towards) the focus of the concave mirror or
appearing to pass through (or directed towards) the focus of a convex mirror.
The reflected ray is parallel to the principal axis.
(iv)
The ray
incident at any angle at the pole. The reflected ray follows laws of
reflection. Figure shows the ray diagram considering three rays. It shows the
image A’B’ (in this case, real) of an object AB formed by a concave mirror. It
does not mean that only three rays emanate from the point A. An infinite number
of rays emanate from any source, in all directions. Thus, point A is image point of A if every ray originating
at point A and falling on the concave mirror after reflection passes through
the point A .
We now derive
the mirror equation or the relation between the object distance (
), image
distance (
) and the focal length (
).
The two right-angled triangles A’B’F and MPF are
similar. (For paraxial rays, MP can be considered to be a straight line
perpendicular to CP.) Therefore
= 
or 
= (∵ PM = AB) ------ (1)
Since ∠ APB = ∠ A’PB’, the right angled
triangles A’B’P and ABP are also similar. Therefore,
= 
------ (2)
Comparing Eqs. (1) and (2) we get,
= 
= ------
(3)
Equation (3) is a
relation involving magnitude of distances. We now apply the sign convention. We
note that light travels from the object to the mirror MPN. Hence this is taken
as the positive direction. To reach the object AB, image A’B’ as well as the focus F from the pole P, we
have to travel opposite to the direction of incident light. Hence, all the
three will have negative signs. Thus,
B’P =
, FP = 
, BP = 
Using these in Eq.
(3) we get ,
= 
= 
From this we can derive the mirror formula as,
+ 
= 
The size of
the image relative to the size of the object is another important quantity to consider.
We define linear magnification (
) as the ratio of the height of the image (
’) to the height
of the object ():
= 
h and h’ will be taken positive or negative in
accordance with the accepted sign convention. In triangles A’B’P and ABP we
have,
=
so that
= = 
This equation
is called the magnification formula.
We have
derived here the mirror equation, and the magnification formula, for the case
of real, inverted image formed by a concave mirror. With the proper use of sign
convention, these are, in fact, valid for all the cases of reflection by a
spherical mirror (concave or convex) whether the image formed is real or
virtual.
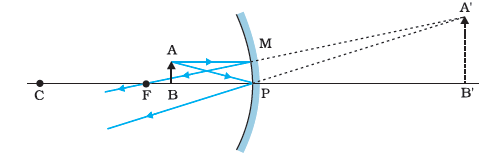
Image
formed by Concave mirror with object between P and F
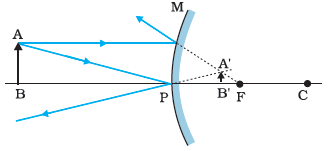
Image
formed by Convex mirror
Locating Images by Drawing Rays
We can graphically locate the
image of any off-axis point of the object by drawing a ray diagram with any two
of four special rays through the point:
1. A ray that is initially
parallel to the central axis reflects through the focal point F (ray 1 in
fig 1)
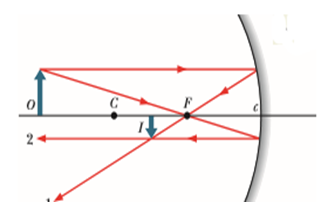
2. A ray that reflects
from the mirror after passing through the focal point emerges parallel to the
central axis (ray 2 in fig 1).
3. A ray that reflects
from the mirror after passing through the center of
curvature C returns along itself (ray 3 in fig 2).
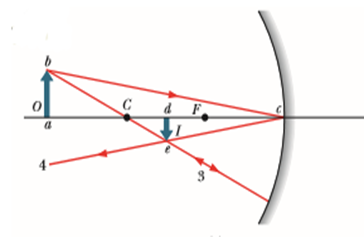
4. A ray that reflects
from the mirror at point c is reflected symmetrically about that axis
(ray 4 in fig 2).
The rules similarly apply for the
convex mirror too.
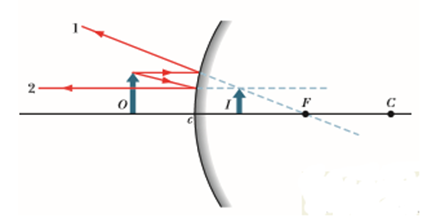
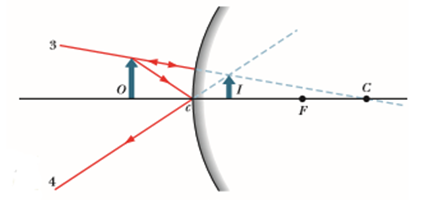
The image of
the point is at the intersection of the two special rays you choose. The
image of the object can then be found by locating the images of two or more of its
off-axis points. You need to modify the descriptions of the rays slightly to
apply them to convex mirrors.
Image formation
by curved mirrors
The table below provides a summary of
how a concave and convex mirror forms images:
|
Position of the
object |
Image formation
by concave mirror |
Image formation
by convex mirror |
|
Object at infinity |
Image formed is
inverted, real, diminished and formed at F. |
Image formed is
upright, virtual and diminished. |
|
Object beyond C |
Image formed is real, inverted and
diminished. |
Image formed is virtual, upright and
diminished. |
|
Object at C |
Image formed is
real, inverted and same size as the object |
Image formed is
virtual, upright and diminished. |
|
Object between C and F |
Image formed is real, inverted and
magnified. |
Image formed is virtual, upright and
diminished. |
|
Object at F |
Image formed is
real, inverted and at infinity. |
Image formed is
virtual, upright and diminished. |
|
Object between F and P |
Image formed is virtual, upright and
magnified. |
Image formed is virtual, upright and
diminished. |
|
|
|
|
