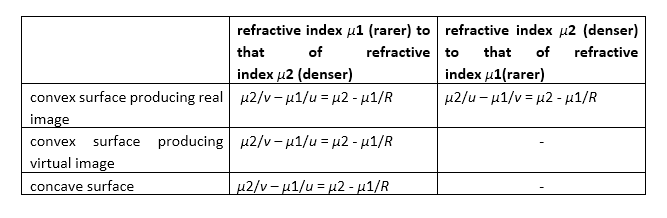
Refraction at a Spherical
Surface
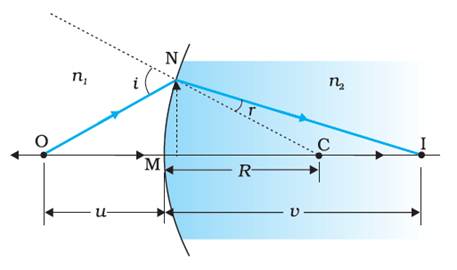
The
above figure shows the geometry of formation of image I of an object O on
the principal axis of a spherical surface with centre
of curvature C, and radius of curvature R. The rays are incident from a medium
of refractive index n1, to another of refractive index n2.
NM will be taken to
be nearly equal to the length of the perpendicular from the point N on the
principal axis. We have, for small angles,
= 
= 
= 
Now for 
, i is exterior angle. Therefore, i = 
i = 
------
(i)
Similarly,
r = 
i.e., r
= 
------
(ii)
Now, by Snell’s law,
or for small angles,
Substituting i and r from equations (i) and (ii),
we get
------
(iii)
Here, OM, MI and MC represent magnitudes of
distances. Applying the cartesian
sign convention,
OM = -u, MI = +v, MC = +R
Substituting these in equation (iii), we get
------
(iv)
Equation (iv) gives us a relation
between object and image distance in terms of refractive index of the medium
and the radius of curvature of the curved spherical surface. It holds for any
curved spherical surface.
