Refraction by Lens

In the above figure (a) shows the geometry of image formation by a double convex lens. It involves two steps,

· Formation of image I₁ of the object O on the refracting surface as shown in (b).

· Image I₁ acts as a virtual object for the second surface that forms the image at I as shown in (c).

Applying (iii) to the first interface ABC, we get,

------ (v)

Applying the same to the interface ADC, we get,

------ (vi)

For thin lens, . On adding both sides of equation (v) and (vi), we get

On simplifying,

)

Since no n₂ terms will be present as each will be cancelled. Hence the equation becomes

) ------ (vii)

Suppose the object is at infinity, i.e., OB = and DI = f. Then the above equation becomes,

) ------ (viii)

The point where image of an object placed at infinity is formed is called the focus F, of the lens and the distance f gives its focal length. A lens has two foci, F and

, on either side of it. This is shown in the below figure for both concave and convex lens.

By sign convention,

BC₁ = + R₁

DC₂ = - R₂

So equation (viii) becomes,

------ (ix)

The above equation is called as len’s markers formula. In that case R₁ is negative, R₂ positive and therefore, f is negative. From equation (vii) and (viii), we get,

------ (x)

BO = – u, DI = +v, we get,

------ (xi)

The above equation is the familiar thin lens formula. Though we derived it for a real image formed by a convex lens, the formula is valid for both convex as well as concave lenses and for both real and virtual images.

It is worth mentioning that the two foci, F and of a double convex or concave lens are equidistant from the optical centre. The focus on the side of the (original) source of light is called the first focal point, whereas the other is called the second focal point.

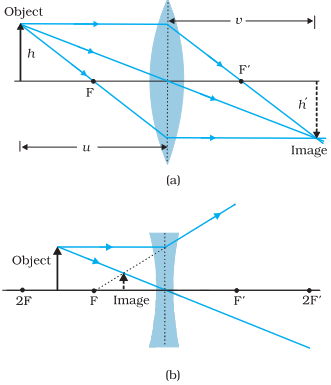
To find the image of an object by a lens, it is convenient to choose any two of the following rays:

i. A ray emanating from the object parallel to the principal axis of the lens after refraction passes through the second principal focus (in a convex lens) or appears to diverge (in a concave lens) from the first principal focus F.

ii. A ray of light, passing through the optical centre of the lens, emerges without any deviation after refraction.

iii. A ray of light passing through the first principal focus (for a convex lens) or appearing to meet at it (for a concave lens) emerges parallel to the principal axis after refraction.

The above image describes these rules for concave and convex lens.

Magnification (m) produced by a lens is defined, like that for a mirror, as the ratio of the size of the image to that of the object. Proceeding in the same way as for spherical mirrors, it is easily seen that for a lens

m = = ------ (xii)

When we apply the sign convention, we see that, for erect (and virtual) image formed by a convex or concave lens, m is positive, while for an inverted (and real) image, m is negative.