Derivation of Kepler's Laws

Kepler Problem: The derivation of the Kepler's three laws of planetary motion from Newton's law of gravitation is called the Kepler problem.

Proof of Kepler's First Law of Planetary Motion:

The planetary motion takes place under the action of the gravitational force exerted by the sun,

=

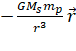
where M_s, is the mass of the sun. This force is radial and central. Negative sign indicates that is oppositely directed to .

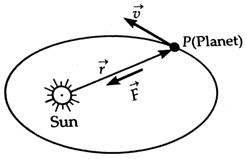
Gravitational force on a planet due to the sun

The torque exerted on the planet P about the sun is

= ×

= ×

= [∵ × = ]

But = Rate of change of angular momentum

=

∴ = 0 or = constant

This shows that the angular momentum of the planet about the sun remains constant both in magnitude and direction. Since the direction of (= × ) is fixed, and lie in a plane normal to . Moreover, it can be shown that the central force under the action of which the planet moves varies as the square of the distance between the planet and sun and this orbit is an ellipse.

Proof of Kepler's Second Law:

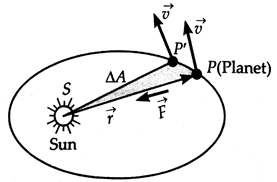
Area swept by the radius vector in time Δt

As shown in above figure, consider a planet moving in an elliptical orbit with the sun at focus S. Let be the position vector of the planet w.r.t. the sun and be the gravitational force on the planet due to the sun. Torque exerted on the planet by this force about the sun is

= ×

= 0 [∵ and are oppositely directed]

But =

∴ = 0 or = constant

Suppose the planet moves from position P to P' in time Δt. The area swept by the radius vector is

Δ = Area of triangular region SPP’

= ×

But = Δ = Δt = Δt

∴ = ( × )

=

= constant [∵ and m are constant]

Thus the areal velocity of the planet remains constant i.e., the radius vector joining planet to the sun sweeps out equal areas in equal intervals of time. This proves Kepler's second law of planetary motion.

Proof of Kepler's Third Law:

Suppose a planet of mass m moves around the sun in a circular orbit of radius r with orbital speed . Let M be the mass of the sun. The force of gravitation between the sun and the planet provides the necessary centripetal force.

∴ = or =

But orbital speed,

=

=

∴ =

Thus α r³

This proves Kepler's third law. The constant K_s is same for all planets. Its value is 2.97 × 10⁻¹⁹ s²m⁻³. For an elliptical orbit, r gets replaced by semi-major axis a.