First Law of Thermodynamics

What is First Law of Thermodynamics?

It states that, “when a certain amount of heat energy is supplied to a system, some part of it is used to perform external work and rest of heat is used to increase the internal energy of the system.”

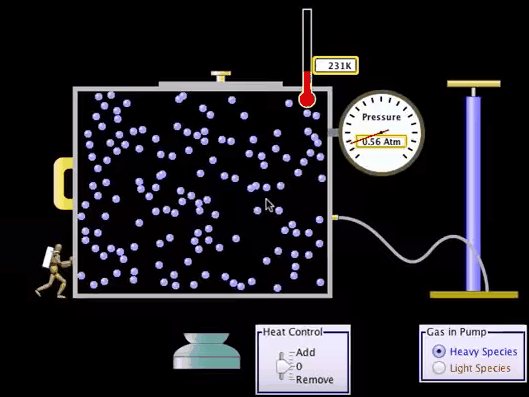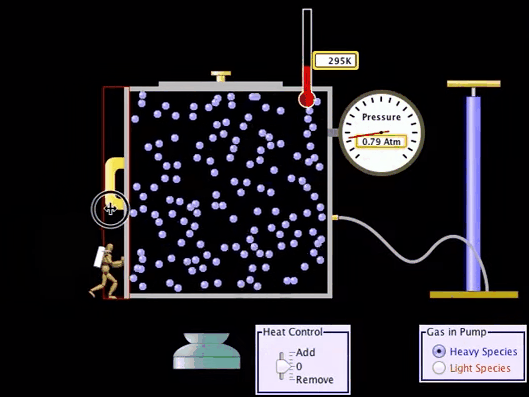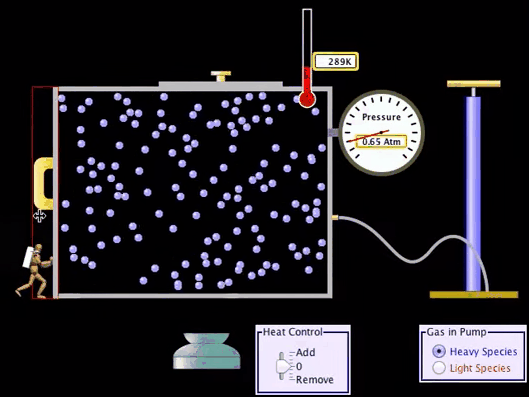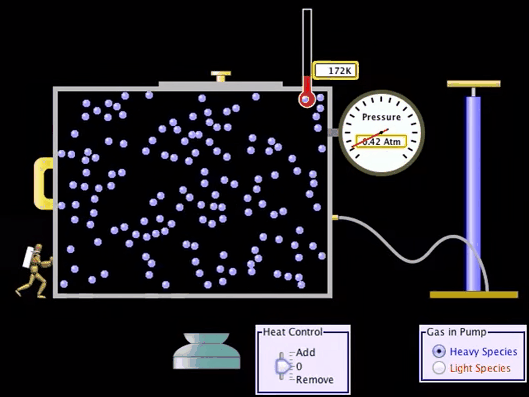
First Law of Thermodynamics

Derivation of First Law of Thermodynamics:

Consider the internal energy U of a system can change through two modes of energy transfer: Heat and Work.

Let Q = Heat supplied to the system by the surroundings

W = Work done by the system on the surroundings

U = Change in internal energy of the system

The general principle of conservation of energy then implies that

Q = U + W ------ (1)

i.e. the energy (Q) supplied to the system goes in partly to increase the internal energy of the system (U) and the rest in work on the environment (W). It is simply the general law of conservation of energy applied to any system in which the energy transfer from or to the surroundings is taken into account.

Let us put Eq. (1) in the alternative form

Q – W = U ------ (2)

Now, the system may go from an initial state to the final state in a number of ways. For example, to change the state of a gas from (P₁, V₁) to (P₂, V₂), first change the volume of the gas from V₁ to V₂, keeping its pressure constant i.e. first go the state (P₁, V₂) and then change the pressure of the gas from P₁ to P₂, keeping volume constant, to take the gas to (P₂, V₂). Alternatively, first keep the volume constant and then keep the pressure constant. Since U is a state variable, U depends only on the initial and final states and not on the path taken by the gas to go from one to the other. Generally Q andW will depend on the path taken to go from the initial to final states.

From the First Law of Thermodynamics, Eq. (2), it is clear that the combination, Q – W is path independent. This shows that if a system is taken through a process in which U = 0.

Q = W

i.e., heat supplied to the system is used up entirely by the system in doing work on the environment. If the system is a gas in a cylinder with a movable piston, the gas in moving the piston does work. Since force is pressure time area, and area time displacement is volume, work done by the system against a constant pressure P is

W = P V

Where V is the change in volume of the gas. Thus, for this case, Eq. (1) gives

Q = U + P V ------ (3)

Change in internal energy for 1 g of water when go from its liquid to vapour phase. The measured latent heat of water is 2256 J/g. i.e., for 1 g of water Q = 2256 J. At atmospheric pressure, 1 g of water has a volume 1 cm³ in liquid phase and 1671 cm³ in vapour phase.

∴ W = P (Vg –Vl)

= 1.013 × 10⁵ × (1671 × 10^–6)

= 169.2 J

Equation (3) then gives

U = 2256 – 169.2

U = 2086.8 J ------ (4)

Thus most of the heat goes to increase the internal energy of water in transition from the liquid to the vapour phase.

Specific Heat Capacity:

Specific heat is defined as the amount of heat required to raise the temperature of a body per unit mass.

It depends on:

· Nature of substance

· Temperature

· Denoted by ‘s’

Mathematically:

s =

where m = mass of the body

ΔQ = amount of heat absorbed or rejected by the substance

ΔT = temperature change

Unit: J kg^–1 K^–1

Example: If we are heating up oil in a pan, more heat is needed when heating up one cup of oil compared to just one tablespoon of oil. If the mass s is more the amount of heat required is more to increase the temperature by one degree.

Molar Specific Heat Capacity:

Molar specific heat capacity of a substance is defined as the amount of heat required to raise the temperature of one gram molecule of the substance through one degree centigrade. It is denoted by C. One mole of substance contains M gram of substance where M is the molecular weight of the substance. So, C = Mc. If n is the number of moles of substance, then,

n =

So, m = nM

Substituting for m in equation,

c =

We get,

c =

Mc =

Thus,  C = Mc =

Specific heat of water is taken to be 1. This is because of the reason for defining unit of heat (calorie) by making use of water.

Heat Capacity or Thermal Capacity:

It is defined as the amount of heat required to raise the temperature of body through 1°C.

If ΔT = 1°C, Q = heat capacity = mc

Q = 

Thus, heat capacity of a body is equal to the product of mass and its specific heat capacity.

Unit: kcal K^-1 or JK^-1

Specific Heat Capacity of Water:

The old unit of heat was calorie. One calorie was earlier defined to be the amount of heat required to raise the temperature of 1g of water by 1°C. With more precise measurements, it was found that the specific heat of water varies slightly with temperature. The following graph shows this variation in the temperature range 0 to 100°C.

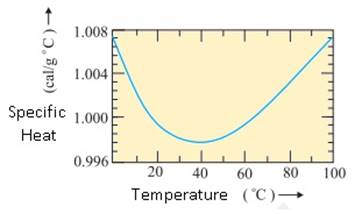
Variation of specific heat capacity of water with temperature.

For a precise definition of calorie, it was, necessary to specify the unit temperature interval. One calorie is defined to be the amount of heat required to raise the temperature of 1g of water from 14.5 °C to15.5 °C. Since heat is just a form of energy, it is preferable to use the unit joule, J.

In SI units, the specific heat capacity of water is 4186 J kg^–1 K^–1 i.e. 4.186 J g^-1 K^–1. The so called mechanical equivalent of heat defined as the amount of work needed to produce 1 cal of heat is in fact just a conversion factor between two different units of energy: calorie to joule. Since in SI units, we use the unit joule for heat, work or any other form of energy, the term mechanical equivalent is now superfluous and need not be used.

As already remarked, the specific heat capacity depends on the process or the conditions under which heat capacity transfer takes place.

Example: For gases, define two specific heats: specific heat capacity at constant volume and specific heat capacity at constant pressure. For an ideal gas, the relation is as follows,

C_P – C_v = R ------ (1)

Where C_P and C_v are molar specific heat capacities of an ideal gas at constant pressure and volume respectively and R is the universal gas constant. To prove the relation, begin with the following equation for 1 mole of the gas:

Q = U + P V

If Q is absorbed at constant volume, V = 0

C_v = = = ------ (2)

Where the subscript v is dropped in the last step, since U of an ideal gas depends only on temperature. (The subscript denotes the quantity kept fixed.) If, Q is absorbed at constant pressure,

C_P = = = ------ (3)

The subscript P can be dropped from the first term since U of an ideal gas depends only on T. Now, for a mole of an ideal gas, which gives

PV = RT

P= R ------ (4)

Equations (2) to (4) give the desired relation, Eq. (1).

Example: Water has highest specific heat of capacity because of which it is used as a coolant in automobile radiators and in hot water bags.

Hot water bag

Water in radiator of the car

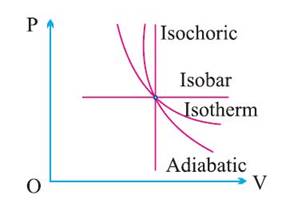
Thermodynamic Processes:

Some special thermodynamic processes:

Type of Processes	Features
Isothermal	Temperature constant
Isobaric	Pressure constant
Isochoric	Volume constant
Adiabatic	No heat flow between the system and the surroundings (Q =0).

Comparison between Isothermal and Adiabatic Changes:

Isothermal Changes	Adiabatic Changes
Temperature (T) remains constant, i.e., ∆T = 0.	Heat content (Q) remains constant, i.e., Q = 0.
System is thermally conducting to the surroundings.	System is thermally insulated from the surroundings.
The changes occurs slowly.	The changes occurs suddenly.
Internal energy (U) remains constant, i.e., U = 0	Internal energy changes, i.e., U ≠ 0
Specific heat becomes infinite.	Specific heat becomes zero.
Equation of isothermal changes is P V = Constant	Equation of adiabatic changes is = Constant
Slope of isothermal curve, = -	Slope of adiabatic curve, = -
Coefficient of isothermal elasticity; Ei = P	Coefficient of adiabatic elasticity; Ea= γ P

Isothermal Process:

What is Isothermal Process?

A process in which the temperature remains constant is called an isothermal process. From the starting of the process till the end, the temperature remains constant.

For the process we have the equation as:

PV = Constant

If a system undergoes changes from the state A to B, considering an isothermal process, the temperature remains constant, i.e., in isothermal surface then,

A - - - - - - - - - - - - isothermal process - - - - -- - -> B

(P₁, V₁, T) (P₂, V₂, T)

Hence P₁V₁ = P₂V₂ = nRT

Isothermal Process

Isothermal Process Examples:

There are various examples of processes where the temperature of the system, some of them are:

· Evaporation is also an example of isothermal process.

· Condensation is an example of isothermal process.

· All the reactions going on in the refrigerator are isothermal as a constant temperature is maintained in it.

· The melting of ice at zero degree is an example of isothermal process.

· The reaction in a heat pump is an example of isothermal process.

· The boiling of water at hundred degrees is an example of isothermal process.

Condition for Isothermal Process:

· The walls of the container must be perfectly conducting.

· The speed of process should be very slow.

Equation of Isothermal Process:

The ideal gas equation for n moles of a gas is

PV = n R ------ (1)

For a fixed mass (n fixed) of a gas undergoing an isothermal process (T fixed), the above equation and in all isothermal process Boyle’s law is obeyed.

Hence equation of state is

PV = constant ------ (2)

This equation is the “equation of state” of an isothermal process.

Indication Diagram:

Done Work in an Isothermal Process:

The pressure of a given mass of gas varies inversely as its volume. This is Boyle’s Law. Suppose an ideal gas goes isothermally (at temperature T) from its initial state (P₁, V₁) to the final state (P₂, V₂). At any intermediate stage with pressure P and volume change from V to V + V (V small)

W = P V

Taking (V <0) and summing the quantity W over the entire process,

W =

= µ RT

∴ Work done = µ RT ln

Where in the second step we have made use of the ideal gas equation PV = RT and taken the constants out of the integral. For an ideal gas, internal energy depends only on temperature. Thus, there is no change in the internal energy of an ideal gas in an isothermal process. The First Law of Thermodynamics then implies that heat supplied to the gas equals the work done by the gas: Q = W.

Q = U + ∆W

Note from the above equation that for V₂ > V₁, W > 0; and for V₂ < V₁, W < 0. That is, in an isothermal expansion, the gas absorbs heat and does work while in an isothermal compression, work is done on the gas by the environment and heat is released.

First Law of Thermodynamics Applied to Isothermal Process:

Applying first law of thermodynamics to an isothermal process

Q =

or

=

· When a gas expands isothermically:

An amount of heat equivalent to the work done by the gas has to be supplied from an external source. & are positive and so will also be positive.

· When a gas compressed isothermically:

An amount of heat equivalent to the work done on the gas has to be removed from the gas.

· In an isothermal compression or expansion, the internal energy of the gas remains unchanged.

Adiabatic Process:

What is Adiabatic Process?

An adiabatic process is a Thermodynamic process in which there is no heat or matter transfer into or out of a system and is generally obtained by surrounding the entire system with a strongly insulating material or by carrying out the process so quickly that there is no time for a significant heat or matter transfer to take place.

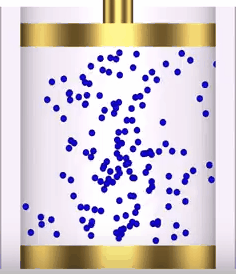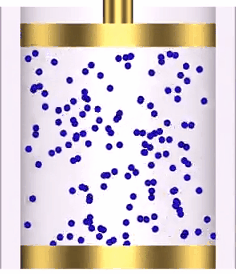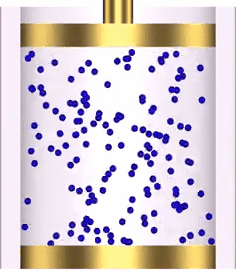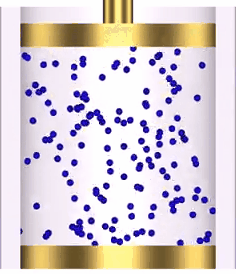
Adiabatic Process

Adiabatic Processes:

· Adiabatic is a process in which there is no heat flow takes place between the system and the surroundings.

· These processes are sudden.

· The walls of the container should be adiabatic.

· For an adiabatic process of an ideal gas.

From Boyle’s law,

PV ^γ = constant

Where γ =  Specific heat ratio.

Example: Hot tea in Thermos flask. It will remain hot as there is no exchange of heat takes place because the walls of thermos is insulating.

Thermal flask

Graphically:

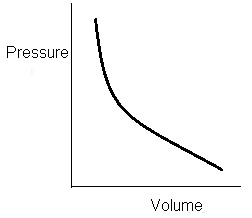
As pressure and volume are inversely proportional we will have decreasing curve. This curve is known as Adiabatic Curve.

Condition for Adiabatic Process:

· All the walls of the container and the piston must be perfectly insulating.

· The speed of process should be fast.

Example of Some Adiabatic Process:

· Sudden bursting of the tube of bicycle tyre.

· Propagation of sound waves in air and other gases.

Energy in Adiabatic Process:

For adiabatic process, ΔQ = 0,

∴ ΔU + ΔW = 0

· If ΔW = positive then ΔU = negative i.e., adiabatic expansion produce cooling.

· If ΔW = negative then ΔU = positive i.e., adiabatic compression produce heating.

Adiabatic Change of an Ideal Gas:

It implies how much work is done during adiabatic change of an ideal gas. Initially ideal gas is at Pressure P₁, Volume V₁ and Temperature T₁ (P₁, V₁, T₁). Final state of an ideal gas Pressure P₂, Volume V₂ and Temperature T₂ (P₂, V₂, T₂)

P V ^γ = constant

γ =

If an ideal gas undergoes a change in its state adiabatically from (P₁, V₁) to (P₂, V₂)

P₁V₁ ^γ = P₂V₂ ^γ

The work done in an adiabatic change of an ideal gas from the state (P₁, V₁, T₁) to the state (P₂, V₂, T₂).

W = ∫ P V Dv

= P∫V dV (Integrating between the limits V₂ and V₁)

For Adiabatic Process:

P V ^γ = constant and this implies P=

W = constant ∫

= constant

=

=

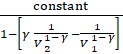
By solving,

Work done W =

where,

T₂ = final Temperature

T₁ = initial temperature

R = Universal gas constant

γ = Specific heat ratio

This is the work done during adiabatic change.

Consider:

W =

Case 1: W>0 (when T₁>T₂)

Temperature of the gas decreases.

Case 2: W< 0 (T₁<T₂)

 Temperature of the gas increases.

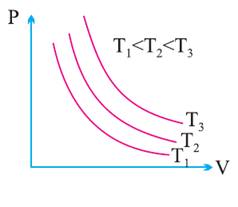
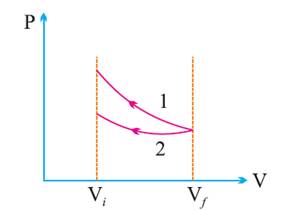
P-V curves for isothermal and adiabatic processes of an ideal gas.

Equation of State:

· Adiabatic relation between P and V: PV^γ = K

· Adiabatic relation between P and T: P^1-γT^γ = K

· Adiabatic relation between T and V: TV^γ-1 = K

Indication Diagram:

Slope of adiabatic curve: tan ϕ = -γ

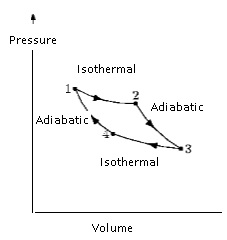
Cyclic and Non-cyclic Process:

A cyclic process consists of a series of changes which return the system back to its initial state. In non-cyclic process the series of changes involved do not return the system back to its initial state.

1. In cyclic process change in internal energy is zero and temperature of system remains constant.

2. Heat supplied is equal to the work done by the system.

3. For cyclic process P–V graph is a closed curve and area enclosed by the closed path represents the work done.

If the cycle is clockwise work done is positive and if the cycle is anticlockwise work done is negative.

Graphical Representation of Various Processes

Heat engine is a device which converts heat into work continuously through a cyclic process.

The essential parts of a heat engine are:

Source: Working substance: Steam, petrol etc.

Sink: ‘‘efficiency’’ η is given by

η =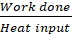

=

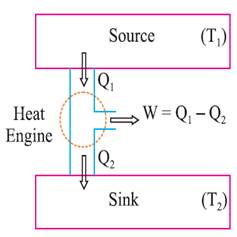
A perfect heat engine η = 1. Practically efficiency is always less than 1

Work Done in an Adiabatic Process:

Consider a unit mole of gas contained in a perfectly non-conducting cylinder provided with a non-conducting and frictionless piston. Let C_v be the specific heat of gas at constant volume. Let at any instant, when the pressure of gas is P, the gas be compressed by small volume dV. Then work done on the gas is,

dW = PdV

Total work done on gas to compress from volume v₁ to v₂ is given by

= W = ------ (1)

According to first law of thermodynamics,

dQ = dU PdV

For adiabatic process, dQ = 0

−dU = PdV = −C_vdT

W =

=

where,

T₁ is the temperature of gas when volume is V₁ and T₂ when volume is V_2.

Thus, work done is given by,

W =

=− C_v(T₂-T₁)

= C_v(T₁-T₂)

W_adi =

The above expression gives us the amount of work done in adiabatic process.