Combination of Resistors

Resistances in Series

Resistors are said to be connected in series, if the same current is flowing through each resistor when some potential difference is applied across the combination.

Current in series combination is same across each resistor

Also,

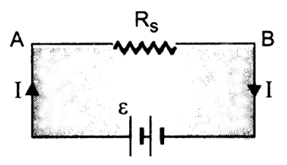
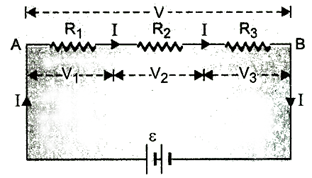
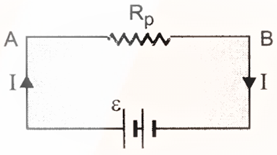
If is the equivalent resistance of the given series combination of resistances, figure, then the potential difference across A and B is,

We have,

or

Resistance in series:- If anumber of resistances are connected in series with each other, the net resistance of the combination is equal to the sum of their individual resistances.           

(a) R = R₁+R₂+R₃

(b) V = V₁+V₂+V₃

(c) I = I₁ = I₂ = I₃ = Constant

(d) V₁ = IR₁, V₂ = IR₂, V₃ = IR₃

Important:

In a series resistance circuit, it should be noted that:

· The current is same in every resistor.

· The current in the circuit is independent of the relative positions of the various resistors in the series.

· The voltage across any resistor is directly proportional to the resistance of the resistor.

· The total resistance of the circuit is equal to the sum of the individual resistances, plus the internal resistance of a cell if any.

· The total resistance in the series circuit is obviously more than the greatest resistance in the circuit.

Resistances in Parallel

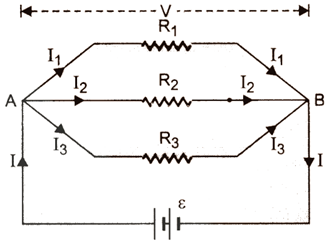
Any number of resistors are said to be connected in parallel if potential difference across each of them is the same and is equal to the applied potential difference.

· Let be the potential difference applied across A and B with the help of a battery ε .

· Let I be the main current in the circuit from battery. I divides itself into three unequal parts because the resistances of these branches are different and be the current through the resistances respectively. Then,

· Here, potential difference across each resistor is V, therefore

or

Putting Values we get,

· If is the equivalent resistance of the given parallel combination of resistance, figure, then

or

We have

Thus, the reciprocal of equivalent resistance of a number of resistor connected in parallel is equal to the sum of the reciprocals of the individual resistances.

Resistance in parallel:- If a number of resistances are connected in parallel, the reciprocal of the resistance of the combination is equal to the sum of the reciprocals of their individual resistances.

(a) 1/R = 1/ R₁ + 1/ R₂ +1/ R₃

(b) I = I₁+I₂+I₃

(c) V = V₁ = V₂ = V₃ = Constant

(d) I₁ = V/R₁, I₂ = V/R₂, I₃ = V/R₃

Important:

In a parallel resistance circuit, it should be noted that:

· The potential difference across each resistor is the same and is equal to the applied potential difference.

· The current through each resistor is inversely proportional to the resistance of that resistor.

· Total current through the parallel combination is the sum of the individual currents through the various resistors.

· The reciprocal of the total resistance of the parallel combination is equal to the sum of the reciprocals of the individual resistances.

The total resistances are connected in series, the current through each resistance is same. When the resistance are in parallel, the pot-diff. across each resistance is the same and not the current.